[선형대수학] Linear Equations in Linear Algebra

인프런 - 선형대수학

 

Linear equation 예시 : Ax = b

 

A system of linear equations = 선형방정식의 시스템(선형시스템, 선형함수)

Linear - 선형

equation - 방정식

solution set - 해의 집합

equivalent - 동치. 두 방정식이 동일한 solution set을 가는 경우.

inconsistent - 해가 없다. 해가 무한이 많다.(기하학적으로 그래프가 겹치는 경우)

consistent - 해가 있다.

coefficient - x의 계수(=A)

coefficient matrix - 계수로만 표현된 행렬

augmented matrix - (증강행렬)계수행렬에  b를 추가한 행렬(계산의 편의성 증가)

scaling - 행에 크기를 곱하는 행위

replacement - 행과 행을 scaling 하여 더하는 개념.  

interchange - 행렬에서 계산의 편의를 위해 행의 순서를 변경하는 행위

row equivalent - 행 동치. 행렬의 모든 행이 동일한 해의 집합을 가진다. consistent 하다.

 

 

 

nonzero row, column - 0으로만 이루어지지 않은 행, 열

A leading entry of row : the leftmost nonzero entry. 행에서 0이 아닌 가장 왼쪽의 원소(계수)

Echelon form(에셀론 폼) : 

1) nonzero 행이 맨 아래 있다.

2) leading entry가 위 행보다 오른쪽에 있다.

Echolon form

 

Reduced echelon form : Echelon form 의 조건 포함. 행렬의 Reduced echelon form은 유일하다. 하나의 형태만 존재한다.

3) 각 행의 leading entry 의 값이 1 이다.

4) leading entry의 열 0 이다.

 

pivot position : position of leading entry

reduced echelon form 예시

 

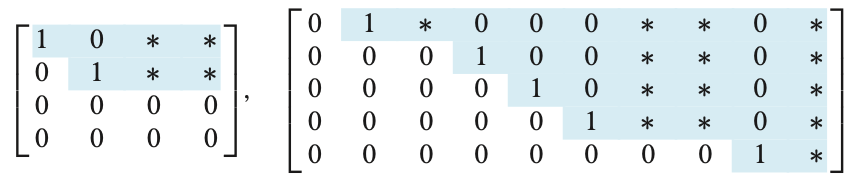
Reduced echelon form : 만들기

첫 행은 pivot column 이다. interchange, replacement 을 반복해서 만든다.

다른 행도 동일한 작업을 반복한다.

echelon form이 완성된다.

마지막 행의 leading entry를 1로 scalling 한다.

그리고 위 행을 interchange, replacement 를 반복하여 leading entry를 1로 만든다. 반복한다.

 

 

basic(leading) variables : 기저 변수

free variables : 방정식(해)에 영향을 주지 않는 변수. (선형 의존)

 

해의 존재와 유일

중요한 정리

해(solutions)가 존재한다면 ~

free variables : 있으면 해가 무한하다.

free variables : 없으면 해가 유한하다.

 

vector equations : 벡터 방정식

vector : 열 벡터를 기본으로 한다. 행 벡터는 열 벡터의 transpose 로 표현

 

벡터의 연산 조건

벡터와 벡터의 덧셈

교환 법칙.

 

벡터와 스칼라 곱(합은 안된다!)

교환 법칙, 분배 법칙

 

 

Linear Combinations : 선형 결합

백터) Rn = [ v1, v2, ..., vp]

스칼라) c = (c1, c2, ..., cp)  -> weights 가중치

선형 결합된 예시

augmented matrix의 해를 구해보자

 

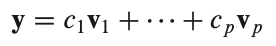
span? 아래 문장은 같은 의미 이다.

is a vector b in span?

dose the following vector wquation have a solution?

dose the following augmented matrix have a solution?

 

벡처 u는 v와 선형 독립일 경우 span이 확장된다

 

 

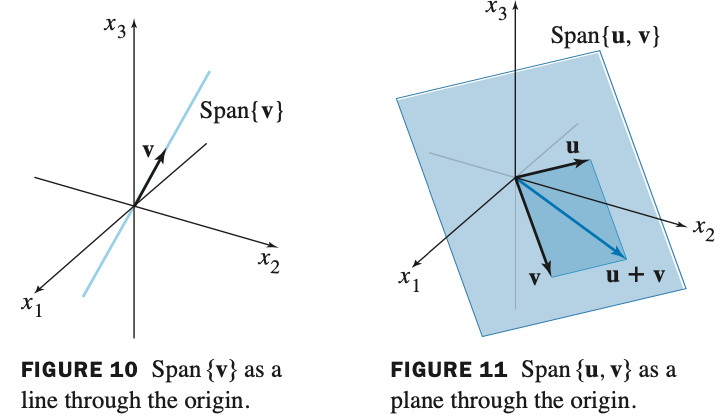
THE MATRIX EQUATION : Ax = b

A = 계수, 가중치, weight

x = 정의역.

행렬 방정식 정의

 

 

vector equation 을 matrix equation 으로 표현

 

정리 3

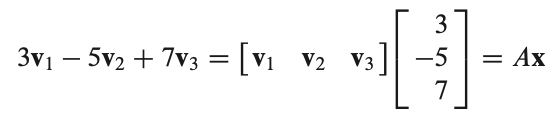
Existence of Solutions

The equation Ax = b has a solution if and only if b is a linear combination of the columns of A.

정리 4

 

 

 

Properties of the Matrix–Vector Product Ax

정리 5

 

SOLUTION SETS OF LINEAR SYSTEMS

Homogeneous Linear Systems : trivial solution 을 포함한 해가 존재 하는 선형 함수. Ax = 0

trivial solution : 해가 0인 경우. (하찮은 해...)

nontrivial solution : trivial solution 외 다른 해

 

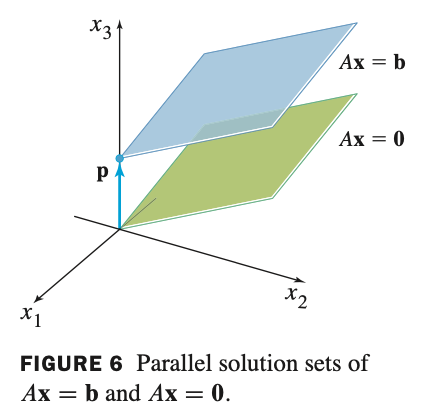
(NonHomogeneous)Ax = b 의 해가 존재 할 때(consistent)

그리고 p 벡터가 하나의 솔루션일 경우

Ax = b 해의 집합이  w = p + vh 로 표현된다.

vh 는 Ax = 0 (Homogeneous)의 임의의 해이다.

 

호모지니어스의 임의의 해를 알면 넌호모지니어스의 방적식의 해(w = p + vh)를 표현할 수 있다.

기하학적으로 해석

 

정리 6

Homogeneous solution 정리6의 기하학적 해석

 

 

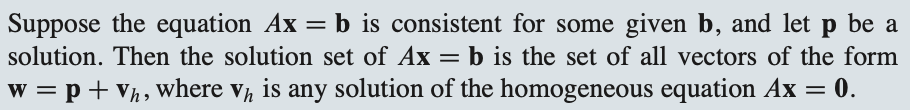
Linearly independent 선형 독립

if and only if : 필요충분 조건.

선형 독립&의존 정의

 

선형독립이라면 trivial solution 하나만 가진다.

 

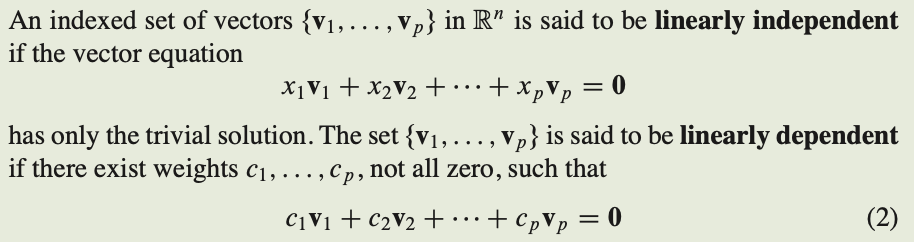
선형 종속 셋의 특징 : 벡터가 다른 벡터로 표현이 가능하다.(예시. x1 = 2*x2)

선형의존의 특징. 정리 7

 

좌) 선형 의존.

우) 선형 독립으로 인해 span을 벗어난다.

정리 7의 기하학적 해석

 

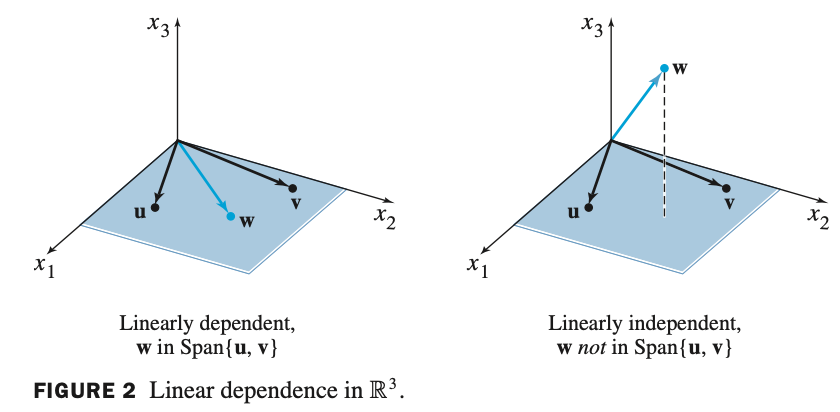
사고를 확장해보자. 네이버 부스트캠프에서도 설명했다.

특징(열)보다 엔트리(행)이 많으면 선형 독립 이다.

예시: 이차원에서 선형독립인 2개의 벡터의 Span은 2차원 전체 이다. 그러므로 3번째 벡터부터는 무조건 선형의존이다.

선형의존 정리 8

 

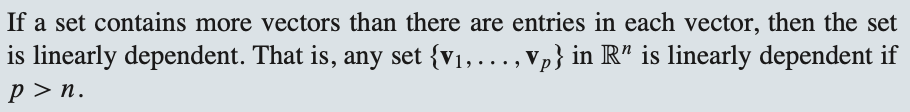
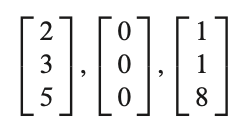
0벡터가 포함될 경우 선형 의존이다.

선형의존 정리 9

 

정리 9의 예시

 

 

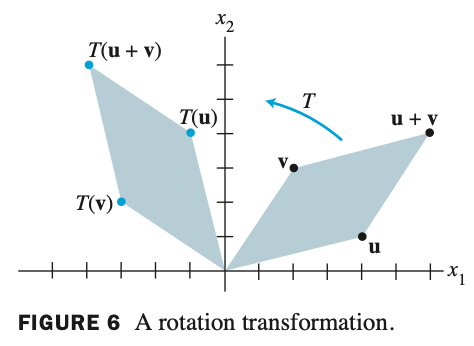
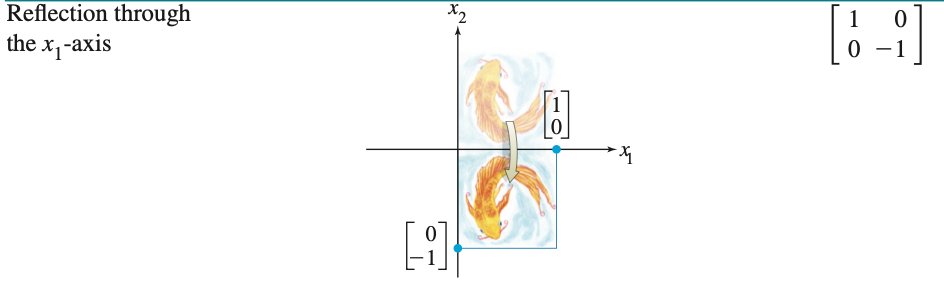
INTRODUCTION TO LINEAR TRANSFORMATIONS

transformation 정의

선형 독립의 경우만 생각한다.

domain : 정의역

codomain : 공의역

range : 치역

 

선형 변환 기하학적 해석

 

예시

 

 

예시2

 

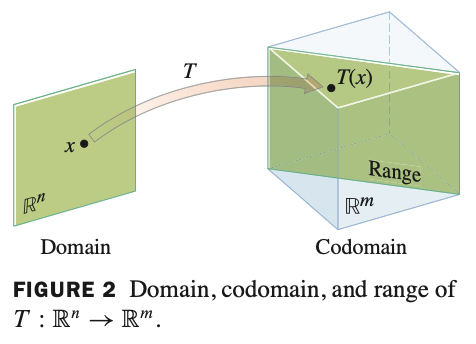
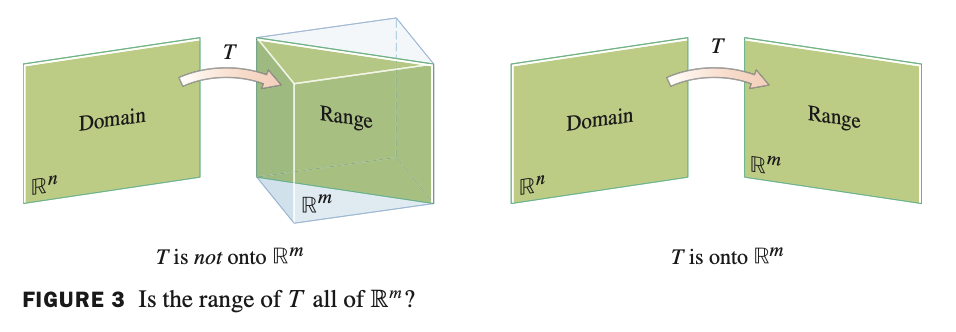
Onto(전사함수) : 공의역==치역

One-to-one(1대1 함수) : 정의역 개수 == 공의역 개수

 

onto 전사함수 정의

 

Onto 설명

One-to-one 1대일1 함수 정의

One-to-one 설명

 

 

 

정리11

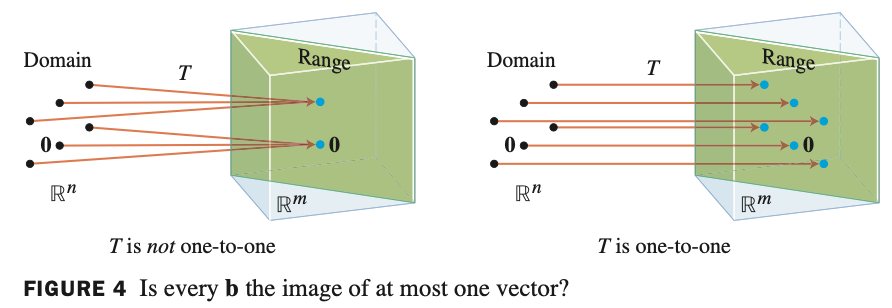
정리4를 참고.

정리12

 

---