모델의 Forward, Backward 구현
import numpy as np
class AffineFunction:
def __init__(self):
self.w = np.random.randn(2)
self.b = np.random.randn()
def forward(self, x):
self.x = x
z = np.dot(self.w, x) + self.b
return z
def backward(self, dJ_dz, LR):
dz_dw = self.x
dz_db = 1
dJ_dw = dJ_dz * dz_dw
dJ_db = dJ_dz * dz_db
self.w -= dJ_dw * LR
self.b -= dJ_db * LR
return dJ_dw
class Sigmoid:
def forward(self, z):
self.pred = 1 / (1 + np.exp(-z))
return self.pred
def backward(self, dJ_dp):
dz_dp = (self.pred * (1 - self.pred))
dJ_dz = dJ_dp * dz_dp
return dJ_dz
class Model:
def __init__(self):
self.affine = AffineFunction()
self.sigmoid = Sigmoid()
def forward(self, x):
z = self.affine.forward(x)
pred = self.sigmoid.forward(z)
return pred
def backward(self, dJ_dp, LR):
dJ_dz = self.sigmoid.backward(dJ_dp)
dJ_dw = self.affine.backward(dJ_dz, LR)
return dJ_dw
class BCELoss:
def forward(self, y, pred):
self.y, self.pred = y, pred
J = -(self.y * np.log(self.pred) + (1 - self.y) * np.log(1 - self.pred))
return J
def backward(self):
dJ_dp = (self.pred - self.y)/(self.pred * (1 - self.pred))
return dJ_dp
파라미터 설정
SEED = 0
np.random.seed(SEED)
N_SAMPLES = 100
LR = 0.25
EPOCHS = 50
DRAW_FREQ = int(EPOCHS / 16)
XOR 데이터셋 생성 - 더 좋은 방법이 없을까...
# XOR 데이터 셋 생성. 개선 필요.
spot = np.linspace(-0.5, 1.5, N_SAMPLES)
x1, x2 = np.meshgrid(spot, spot)
x2 = x2[::-1]
x1, x2 = x1.flatten(), x2.flatten()
w_ = 0.5
y = []
for x1_, x2_ in zip(x1, x2):
z_ = w_*x1_ + w_*x2_
if (z_ > 0.25) and (z_ < 0.75): y.append(1)
else: y.append(0)
y = np.array(y)
XOR 모델 생성 및 학습
import matplotlib.pyplot as plt
# 모델 생성
m_nand = Model()
m_or = Model()
m_and = Model()
bce = BCELoss()
bcelosses = []
accuracies = []
threshold = 0.5
TP = 0
FN = 0
FP = 0
TN = 0
fig, axes = plt.subplots(4, 4, figsize=(10,10))
axes = axes.flatten()
for epoch in range(EPOCHS):
epoch_loss = 0
y_db = []
for x1_, x2_, y_ in zip(x1, x2, y):
# predict
p1 = m_nand.forward(np.array([x1_, x2_]))
p2 = m_or.forward(np.array([x1_, x2_]))
pred = m_and.forward(np.array([p1, p2]))
# BCELoss
j = bce.forward(y_, pred)
epoch_loss += j
# Backpropagation
dJ_dp = bce.backward()
dJ_dw = m_and.backward(dJ_dp, LR)
m_nand.backward(dJ_dw[0], LR)
m_or.backward(dJ_dw[1], LR)
# confusion matrix
if (pred > threshold) and (y_ == 1): TP += 1
elif (pred <= threshold) and (y_ == 1): FN += 1
elif (pred > threshold) and (y_ == 0): FP += 1
else: TN += 1
if epoch % DRAW_FREQ == 0 and epoch > 1:
y_db = []
for x1_, x2_, y_ in zip(x1, x2, y):
p1 = m_nand.forward(np.array([x1_, x2_]))
p2 = m_or.forward(np.array([x1_, x2_]))
pred = m_and.forward(np.array([p1, p2]))
y_db.append(pred)
axes[(epoch // DRAW_FREQ)-1].scatter(x1, x2, c=y_db, cmap='bwr')
bcelosses.append(epoch_loss/(N_SAMPLES**2))
accuracy = (TP + TN)/(TP + FN + FP + TN)
accuracies.append(accuracy)
fig, axes = plt.subplots(3, 1, figsize=(10, 10))
axes[0].scatter(x1, x2, c=y, cmap='bwr')
axes[0].set_ylabel('Data Scatter')
axes[1].plot(bcelosses)
axes[1].set_ylabel('BCELoss')
axes[1].axhline(min(bcelosses), color='lightgray', linestyle='--')
axes[2].plot(accuracies)
axes[2].set_ylabel('Accuracy')
axes[2].set_xlabel('Epoch')
axes[2].axhline(max(accuracies), color='lightgray', linestyle='--')
fig.tight_layout()
학습 과정 시각화
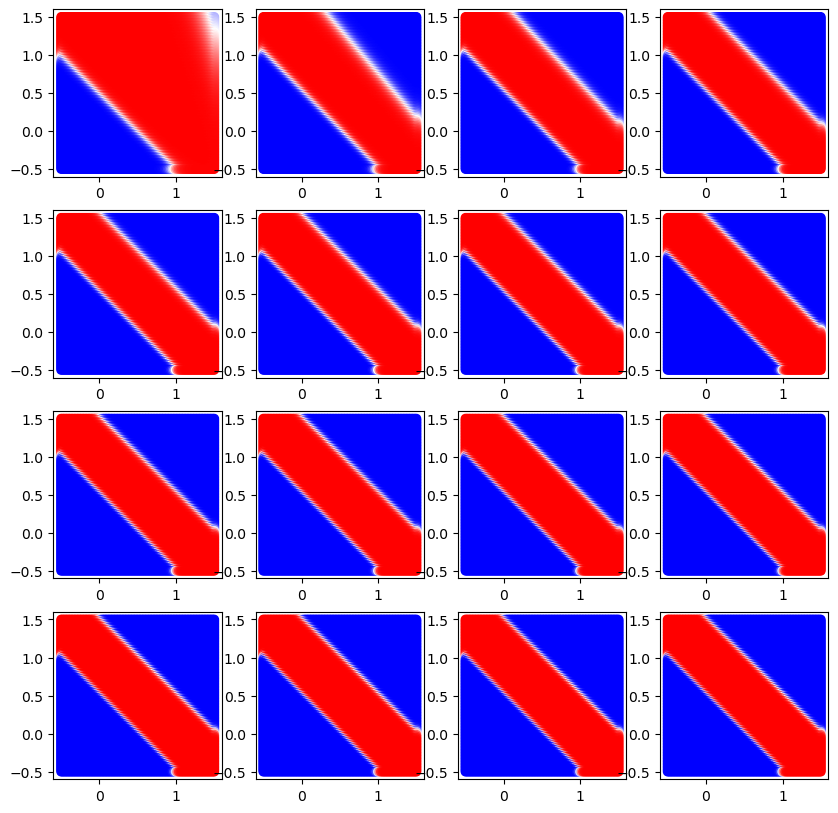
학습 결과

'개발 > AI' 카테고리의 다른 글
| [Pytorch] Multiclass Classification : 임의의 클러스터 학습 (1) | 2023.11.21 |
|---|---|
| [Pytorch] XOR 학습 (0) | 2023.11.20 |
| [Python] Affine, Sigmoid, BCELoss 구현 (0) | 2023.11.14 |
| [Python] GBL : Gradient-based Learning (1) | 2023.11.13 |
| [Python] Backpropagation (1) | 2023.11.13 |